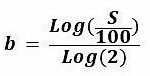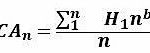Besonders im High-Mix/Low-Volume Bereich können die Kosten des Fertigungsprozesses stärker durch Lerneffekte beeinflusst sein als durch einmalige Rüstkosten.
Herkunft des Modells der Lernkurve
Das mathematische Modell der Lernkurve ist zum ersten Mal durch Theodore Paul Wright 1936 vorgestellt worden und hat Beliebtheit in der Flugzeugproduktion während des 2. Weltkrieges gewonnen. Wright beobachtete, dass bei sich wiederholenden Arbeitsschritten die Zeit für die Durchführung eines einzelnen Arbeitsschrittes kontinuierlich sinkt. Anfänglich ist der Lerneffekt recht stark und resultiert in einer hohen Zeiteinsparung, bei hohen Fertigungszahlen des Fertigungsprozesses wird jedoch kaum noch eine zusätzliche Zeiteinsparung erzielt, da die Arbeitskräfte nahe ihrer maximalen Effizienz arbeiten. Dies ist der Grund, warum gerade bei kleineren Produktionsgrößen der Lerneffekt verhältnismäßig stärker wirkt als bei großen Produktionsvolumen.
Während die Lernkurve in maschinellen Fertigungsprozessen wahrscheinlich nicht auftreten wird, ist ihre Relevanz bei weniger automatisieren Prozessen deutlich. Das Sinken des Zeitbedarfes und damit der Arbeitskosten bei weniger automatisierten Prozessen ist von entscheidender Bedeutung, wenn z. B. genaue Preise zu bestimmen, Produktionserwartungen festzulegen, Produktionszeitpläne oder Mitarbeiterschichten zu planen sind.
Methoden zur Berücksichtigung der Lernkurve in der Fertigung
Standardmengenansatz
Diese Methode beruht auf der Verwendung einer geschätzten Standardmenge, die am häufigsten vom Unternehmen angeboten wird, um den Zeitbedarf für einen Fertigungsschritt zu bestimmen. Beispielsweise wird bei einer typische Fertigungsgröße von 50 Einheiten für die manuelle Sichtprüfung ein Zeitbedarf von 3 Minuten je Fertigungseinheit ermittelt. Bei Verwendung dieser Methode wird das Angebotsmodell 3 Minuten pro Einheit benötigen, unabhängig davon, ob das Angebot für 5, 50 oder 500 Einheiten gilt.
Der Nachteil dieses Ansatzes besteht darin, dass der kalkulierte Preis für 5 Baugruppen die Kosten für die Durchführung der Sichtprüfung nicht richtig erfasst. Durch die geringere Anzahl wird der Zeitbedarf je Fertigungseinheit unterschätzt. Umgekehrt ist der Preis für 500 Einheiten nicht wettbewerbsfähig, da die Sichtprüfung pro Baugruppe weniger Zeit in Anspruch nimmt, wenn sich die Produktionszahl erhöht.
Stufenweise Reduzierung
Diese Methode definiert Mengenbereiche um den Zeitbedarf zu bestimmen. Bei wachsenden Fertigungsmengen sinkt der Zeitbedarf je Einheit, sobald eine neue Stufe erreicht wird. Während diese Methode zwar die Zeitbedarfe präziser betrachtet, entstehen dennoch Ungenauigkeiten innerhalb der einzelnen Bereiche. Dieses liegt daran, dass sie in ihrer einfachen Form den Standardmengenansatz innerhalb der Mengenbereiche anwendet, was zu den exakt gleichen Problemen an den jeweiligen unteren und oberen Intervallgrenzen führt.
Bei 11 Einheiten könnten beispielsweise 4 Minuten je Baugruppe nicht ausreichen, um den Zeitbedarf der Sichtkontrolle zu decken und bei 25 Einheiten könnten 4 Minuten bereits zu viel sein. Es führt auch zu nicht nachvollziehbaren Step-Down-Effekten, bei dem die Kosten für die Fertigung der Gesamtmenge plötzlich sinken kann, wenn sich die Gesamtmenge erhöht. Dieses ist zum Beispiel beim Schritt von 25 zu 26 Einheiten der Fall.
Kumulative durchschnittliche Lernkurve
Die Berechnung der kumulativen durchschnittlichen Lernkurve (CA) wendet grundlegende Prinzipien der Differentialrechnung an, um einen gleitenden Übergang zwischen den Fertigungsgrößen zu erstellen. Die Anwendung dieses Konzepts ist hilfreich, da es im Gegensatz zur vorherigen Methode die beschriebenen Ungenauigkeiten an den Intervallgrenzen vermeidet und den Zeitaufwand präzise für jede einzelne Fertigungsgröße errechnen kann.
Exogene Variablen:
Um die CA-Lernkurve aufzustellen müssen folgende Variablen festgelegt werden:
- n = Anzahl der zu bauenden Einheiten
- S = Lerngeschwindigkeit auf einer Skala von 1 bis 100, wobei 100 für kein Lernen steht und ein niedrigerer Wert von S für eine schnellere Lerngeschwindigkeit
- H1 = Zeit für den Aufbau der 1. Einheit ohne Lernen
Endogene Variablen:
Folgende Variablen werden mit Hilfe des Modells ermittelt:
- Hn = Zeit für die Erstellung der n-ten Einheit
- b = Lernsteigung
- CAn = kumulative Durchschnittszeit für 1 bis n Stück
Ähnlich wie bei anderen Methoden zur Ermittlung des Lernens ist die größte Herausforderung bei der Verwendung dieser Gleichung die Bestimmung des Wertes von S, der Lerngeschwindigkeit. Die meisten EMS-Unternehmen würden S zwischen 80 bis 100 wählen wollen, um typische Lernraten der Arbeitsschritte für die elektronische Auftragsfertigung darzustellen. Ähnlich wichtig ist aber auch die Wahl des Zeitansatzes für den Bau der ersten Einheit (H1), da dieses den Schnittpunkt des Graphen an der Ordinatenachse bestimmt. Sobald diese beiden Variablen definiert sind, lässt sich mit Hilfe der Gleichung aus dem darauffolgenden Schritt der Wert für Hn – also der Zeitbedarf für die Produktion der n-ten Einheit – ermitteln. Um schließlich die kumulative Durchschnittszeit für den Bau von n Einheiten zu erhalten, sollte einfach der Durchschnittswert für H1, H2, H3, …Hn verwendet werden.
Schritt eins: Berechnung der Lernsteigung:
Schritt zwei: Bestimmung der Zeit für den Aufbau der n-ten Einheit:
Schritt drei: Ermittlung des kumulativen Durchschnitts:
Wie beschrieben gibt es mehrere Möglichkeiten, wie EMS-Unternehmen die Lernkurve berücksichtigen können. Es ist wichtig zu beachten, dass externe Faktoren wie menschliches Verhalten oder technologische Innovation die Lernkurve der zu messenden Aktivität beeinflussen können. Letztendlich bleibt die Lernkurve immer noch ein Prognoseinstrument, wenn auch ein präzises.
Umsetzung
Um die Lernkurve in den jeweiligen Kalkulationsprozess einzuführen, kann diese als Excel ausgearbeitet, als Funktion in die kundenspezifische Software eingebettet oder eine Plattform von Drittanbietern, wie bspw. das Arbeitsmodul von QuoteCQ, genutzt werden. Nach der Kalkulation können die so ermittelten aggregierten Zeitbedarfe der jeweiligen Arbeitsschritte als Arbeitskosten in das Fertigungsangebot aufgenommen werden. So kann den Kunden ein konkurrenzfähiges sowie gleichzeitig profitables Angebot unterbreitet werden.
Der nächste Schritt ist nun die Suche nach Möglichkeiten zur Erhöhung der Lernrate. Die Verbesserung der Prozesse und die schnelle Umsetzung neuer Techniken bringt einen erheblichen Wettbewerbsvorteil. Neue Schulungsansätze, die Bereitstellung besserer Werkzeuge und die allgemeine Verbesserung der Arbeitsabläufe in der Produktion kann langfristig einen enormen Vorteil gegenüber dem Wettbewerb darstellen.
Die Einführung der Lernkurve in den Angebotsprozess wird dazu beitragen, konkurrenzfähig und profitabel Geschäfte anzubieten.
Hier finden Sie mehr über: